Basic PvSTATEM functionalities

Reading the plate object

The basic functionality of the PvSTATEM package is reading raw MBA data. To present the package’s functionalities, we use a sample dataset from the Covid OISE study, which is pre-loaded into the package. You might want to replace these variables with paths to your files on your local disk. Firstly, let us load the dataset as the plate object.

library(PvSTATEM)

plate_filepath <- system.file("extdata", "CovidOISExPONTENT.csv", package = "PvSTATEM", mustWork = TRUE) # get the filepath of the csv dataset

layout_filepath <- system.file("extdata", "CovidOISExPONTENT_layout.xlsx", package = "PvSTATEM", mustWork = TRUE)


plate <- read_luminex_data(plate_filepath, layout_filepath) # read the data

#> Reading Luminex data from: /home/runner/work/_temp/Library/PvSTATEM/extdata/CovidOISExPONTENT.csv
#> using format xPONENT
#> 
#> New plate object has been created with name: CovidOISExPONTENT!
#>

plate

#> Plate with 96 samples and 30 analytes

Processing the whole plate

Once we have loaded the plate object, we may process it using the function process_plate. This function fits a model to each analyte using the standard curve samples. It computes RAU values for each analyte using the corresponding model. The computed RAU values are then saved to a CSV file in a specified folder, with a specified name, which by default is based on the plate name and the normalisation type - this function also allows normalisation for nMFI values, more details about this method may be found in the nMFI section of this document, or in documentation of ?get_nmfi function.

To get more information about the function, check ?process_plate.

example_dir <- tempdir(check = TRUE) # create a temporary directory to store the output
df <- process_plate(plate, output_dir = example_dir)

#> Fitting the models and predicting RAU for each analyte
#> Adding the raw MFI values to the output dataframe
#> Saving the computed RAU values to a CSV file located in: '/tmp/RtmppxGliI/CovidOISExPONTENT_RAU.csv'

colnames(df)

#>  [1] "Spike_6P"          "ME"                "HKU1_S"           
#>  [4] "OC43_NP"           "OC43_S"            "HKU1_NP"          
#>  [7] "X229E_NP"          "Mumps_NP"          "RBD_B16171"       
#> [10] "NL63_NP"           "RBD_B16172"        "RBD_wuhan"        
#> [13] "NL63_S"            "X229E_S"           "Spike_B16172"     
#> [16] "Spike_B117"        "Measles_NP"        "Ade5"             
#> [19] "NP"                "Spike_P1"          "Rub"              
#> [22] "Ade40"             "RBD_B117"          "Spike_B1351"      
#> [25] "FluA"              "RBD_B1351"         "RBD_P15"          
#> [28] "S2"                "Spike_omicron"     "RBD_omicron"      
#> [31] "Spike_6P_raw"      "ME_raw"            "HKU1_S_raw"       
#> [34] "OC43_NP_raw"       "OC43_S_raw"        "HKU1_NP_raw"      
#> [37] "X229E_NP_raw"      "Mumps_NP_raw"      "RBD_B16171_raw"   
#> [40] "NL63_NP_raw"       "RBD_B16172_raw"    "RBD_wuhan_raw"    
#> [43] "NL63_S_raw"        "X229E_S_raw"       "Spike_B16172_raw" 
#> [46] "Spike_B117_raw"    "Measles_NP_raw"    "Ade5_raw"         
#> [49] "NP_raw"            "Spike_P1_raw"      "Rub_raw"          
#> [52] "Ade40_raw"         "RBD_B117_raw"      "Spike_B1351_raw"  
#> [55] "FluA_raw"          "RBD_B1351_raw"     "RBD_P15_raw"      
#> [58] "S2_raw"            "Spike_omicron_raw" "RBD_omicron_raw"

We can take a look at a slice of the produced dataframe (as not to overcrowd the article).

df[1:5, 1:5]

#>                Spike_6P        ME     HKU1_S   OC43_NP     OC43_S
#> CO-F-226-01-CF 20000.00  5768.628   829.2993 4289.2647  6871.6113
#> CO-F-263-02-KC 20000.00  4050.148  8128.2569 3681.9063  8828.6351
#> CO-F-080-02-TV 20000.00  5889.229 15877.9572 1473.4541 11012.7498
#> CO-F-215-01-BA 20000.00 10446.952  6069.3115  828.9687  1116.0059
#> CO-H-SD-039-BC 17665.36  2656.989  4055.8890  990.4044   670.7302

Quality control and normalisation details

Apart from the process_plate function, the package provides a set of methods allowing for more detailed and advanced quality control and normalisation of the data.

Plate summary and details

After the plate is successfully loaded, we can look at some basic information about it.

plate$summary()

#> Summary of the plate with name 'CovidOISExPONTENT':
#> Plate examination date: 2022-05-11 16:45:00
#> Total number of samples: 96
#> Number of blank samples: 1
#> Number of standard curve samples: 11
#> Number of positive control samples: 0
#> Number of negative control samples: 0
#> Number of test samples: 84
#> Number of analytes: 30

plate$summary(include_names = TRUE) # more detailed summary

#> Summary of the plate with name 'CovidOISExPONTENT':
#> Plate examination date: 2022-05-11 16:45:00
#> Total number of samples: 96
#> Number of blank samples: 1
#> Number of standard curve samples: 11
#> Sample names: '1/50', '1/100', '1/200', '1/400', '1/800', '1/1600', '1/3200', '1/6400', '1/12800', '1/25600', '1/102400'
#> Number of positive control samples: 0
#> Number of negative control samples: 0
#> Number of test samples: 84
#> Number of analytes: 30

plate$sample_names

#>  [1] "B"              "1/50"           "1/100"          "1/200"         
#>  [5] "1/400"          "1/800"          "1/1600"         "1/3200"        
#>  [9] "1/6400"         "1/12800"        "1/25600"        "1/102400"      
#> [13] "CO-F-226-01-CF" "CO-F-263-02-KC" "CO-F-080-02-TV" "CO-F-215-01-BA"
#> [17] "CO-H-SD-039-BC" "CO-H-RD-053-MO" "CO-F-030-01-LA" "CO-F-204-01-TC"
#> [21] "CO-F-009-01-CS" "CO-F-156-02-GB" "CO-F-402-03-DE" "CO-H-SK-021-BC"
#> [25] "CO-F-226-02-CM" "CO-F-266-01-LC" "CO-F-080-03-TA" "CO-F-215-02-BN"
#> [29] "CO-H-SD-042-DD" "CO-H-RK-002-BA" "CO-F-031-01-LD" "CO-F-204-02-TT"
#> [33] "CO-F-021-03-DF" "CO-F-156-03-GN" "CO-F-402-04-DR" "CO-H-SK-023-DC"
#> [37] "CO-F-226-03-CG" "CO-F-272-01-DF" "CO-F-080-04-TM" "CO-F-215-03-BA"
#> [41] "CO-H-SK-004-GA" "CO-H-RK-004-WN" "CO-F-112-01-CN" "CO-F-220-01-VV"
#> [45] "CO-F-028-01-PJ" "CO-F-214-01-SP" "CO-F-402-05-DS" "CO-H-SK-029-LC"
#> [49] "CO-F-234-01-LC" "CO-F-310-01-DC" "CO-F-082-01-OF" "CO-F-299-01-CS"
#> [53] "CO-H-SK-006-MS" "CO-H-RK-007-CJ" "CO-F-180-01-PN" "CO-F-243-01-BL"
#> [57] "CO-F-124-01-SV" "CO-F-237-01-LE" "CO-H-SD-002-WL" "CO-H-SK-030-MJ"
#> [61] "CO-F-234-02-LS" "CO-F-311-01-PC" "CO-F-089-01-DP" "CO-F-325-01-LN"
#> [65] "CO-H-SK-011-CC" "CO-H-RK-009-MB" "CO-F-180-02-DM" "CO-F-243-02-SH"
#> [69] "CO-F-134-01-MK" "CO-F-281-01-BV" "CO-H-SD-013-LV" "CO-H-SK-031-CP"
#> [73] "CO-F-260-01-GD" "CO-F-075-01-BA" "CO-F-089-02-DC" "CO-H-SD-004-CG"
#> [77] "CO-H-SK-051-DA" "CO-H-RK-010-VP" "CO-F-180-03-DR" "CO-F-276-01-ME"
#> [81] "CO-F-134-02-GM" "CO-F-402-01-BH" "CO-H-SD-043-BS" "CO-H-SK-039-AA"
#> [85] "CO-F-260-02-GC" "CO-F-075-02-FM" "CO-F-139-01-BP" "CO-H-SD-021-PC"
#> [89] "CO-H-SK-056-MN" "CO-F-027-02-SL" "CO-F-180-04-DC" "CO-F-027-01-SF"
#> [93] "CO-F-156-01-GA" "CO-F-402-02-DV" "CO-H-SK-018-VC" "CO-F-045-01-SN"

plate$analyte_names

#>  [1] "Spike_6P"      "ME"            "HKU1_S"        "OC43_NP"      
#>  [5] "OC43_S"        "HKU1_NP"       "X229E_NP"      "Mumps_NP"     
#>  [9] "RBD_B16171"    "NL63_NP"       "RBD_B16172"    "RBD_wuhan"    
#> [13] "NL63_S"        "X229E_S"       "Spike_B16172"  "Spike_B117"   
#> [17] "Measles_NP"    "Ade5"          "NP"            "Spike_P1"     
#> [21] "Rub"           "Ade40"         "RBD_B117"      "Spike_B1351"  
#> [25] "FluA"          "RBD_B1351"     "RBD_P15"       "S2"           
#> [29] "Spike_omicron" "RBD_omicron"

The summary can also be accessed using the built-in generic method summary.

summary(plate)

#> Summary of the plate with name 'CovidOISExPONTENT':
#> Plate examination date: 2022-05-11 16:45:00
#> Total number of samples: 96
#> Number of blank samples: 1
#> Number of standard curve samples: 11
#> Number of positive control samples: 0
#> Number of negative control samples: 0
#> Number of test samples: 84
#> Number of analytes: 30

Quality control

The package can plot the RAU along the MFI values, allowing manual inspection of the standard curve. This method raises a warning in case the MFI values were not adjusted using the blank samples.

plot_standard_curve_analyte(plate, analyte_name = "OC43_S")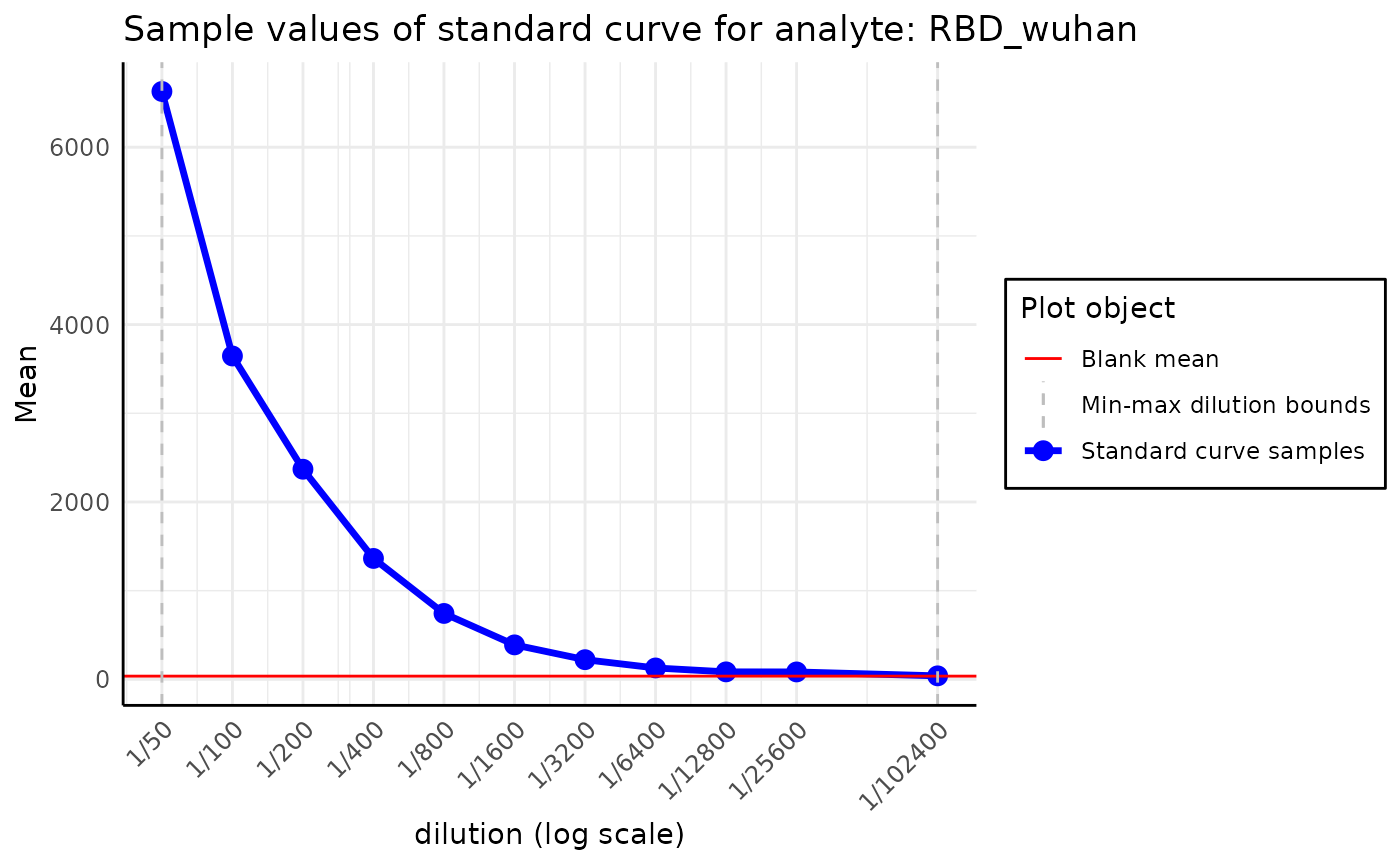

plate$blank_adjustment()

#> Plate with 96 samples and 30 analytes

print(plate$blank_adjusted)

#> [1] TRUE

plot_standard_curve_analyte(plate, analyte_name = "OC43_S")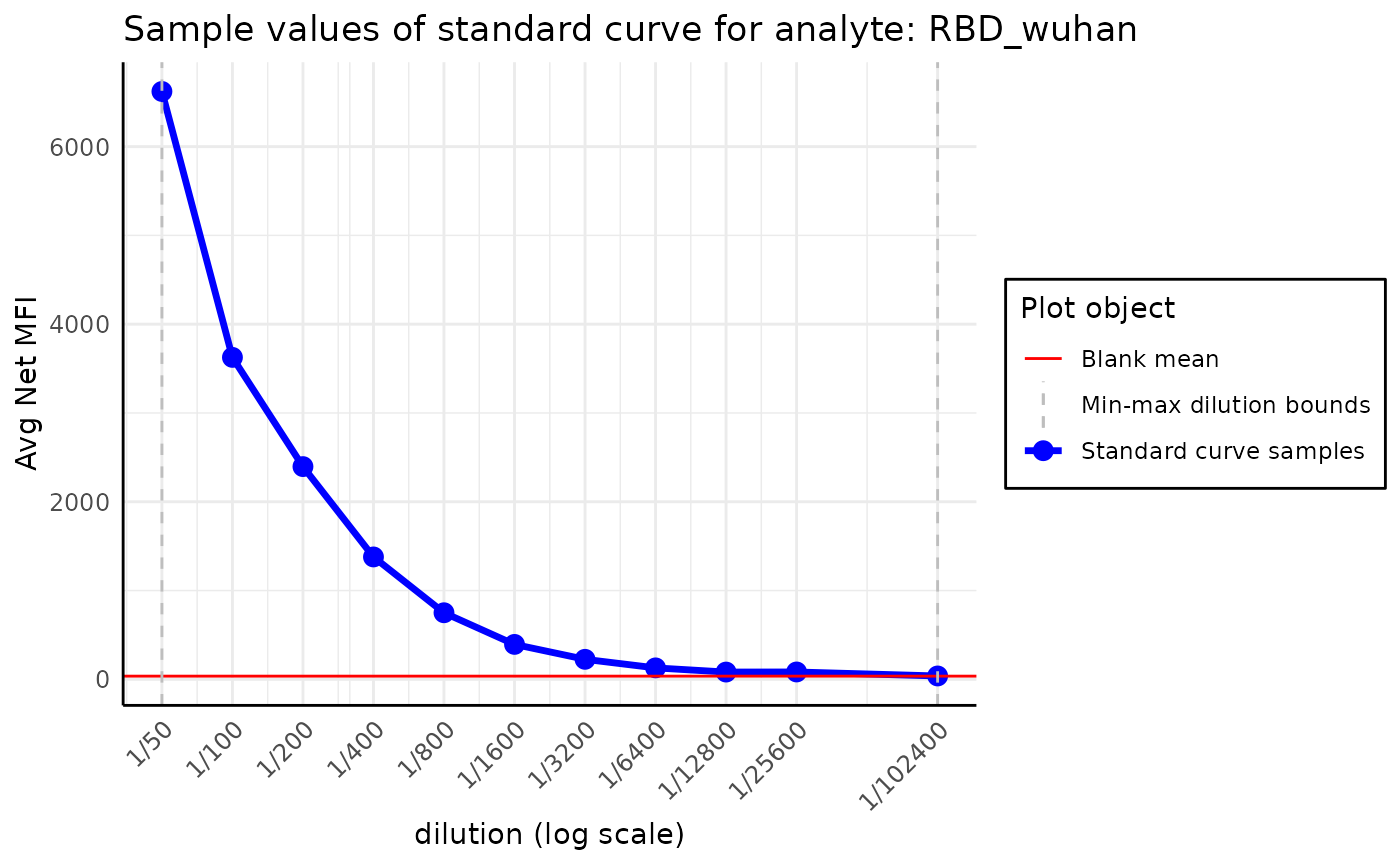

We can also plot the standard curve for different analytes and data types. A list of all available analytes on the plate can be accessed using the command plate$analyte_names.

By default, all the operations are performed on the Median value of the samples; this option can be selected from the data_type parameter of the function.

plot_standard_curve_analyte(plate, analyte_name = "RBD_wuhan", data_type = "Mean")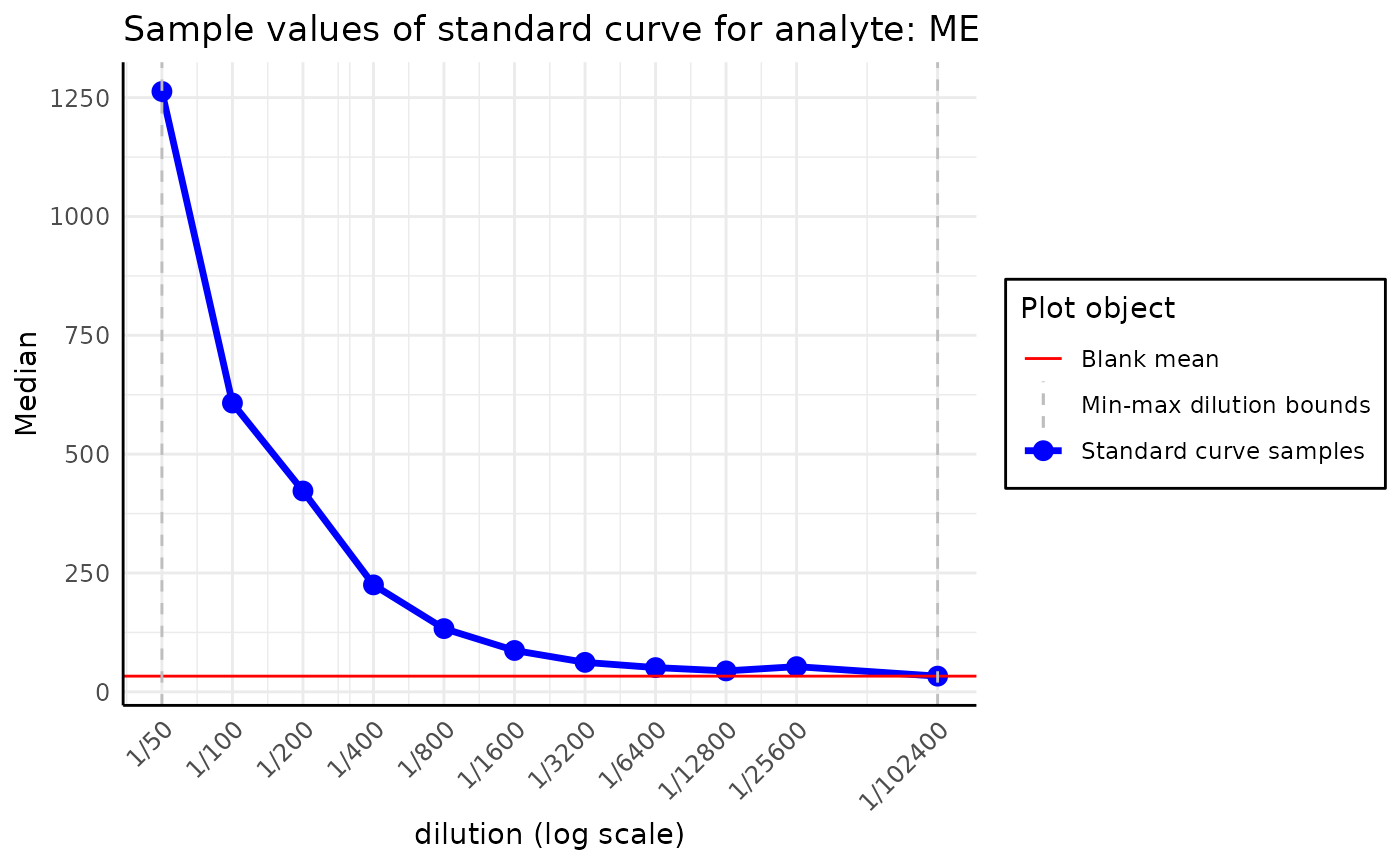

plot_standard_curve_analyte(plate, analyte_name = "RBD_wuhan", data_type = "Avg Net MFI")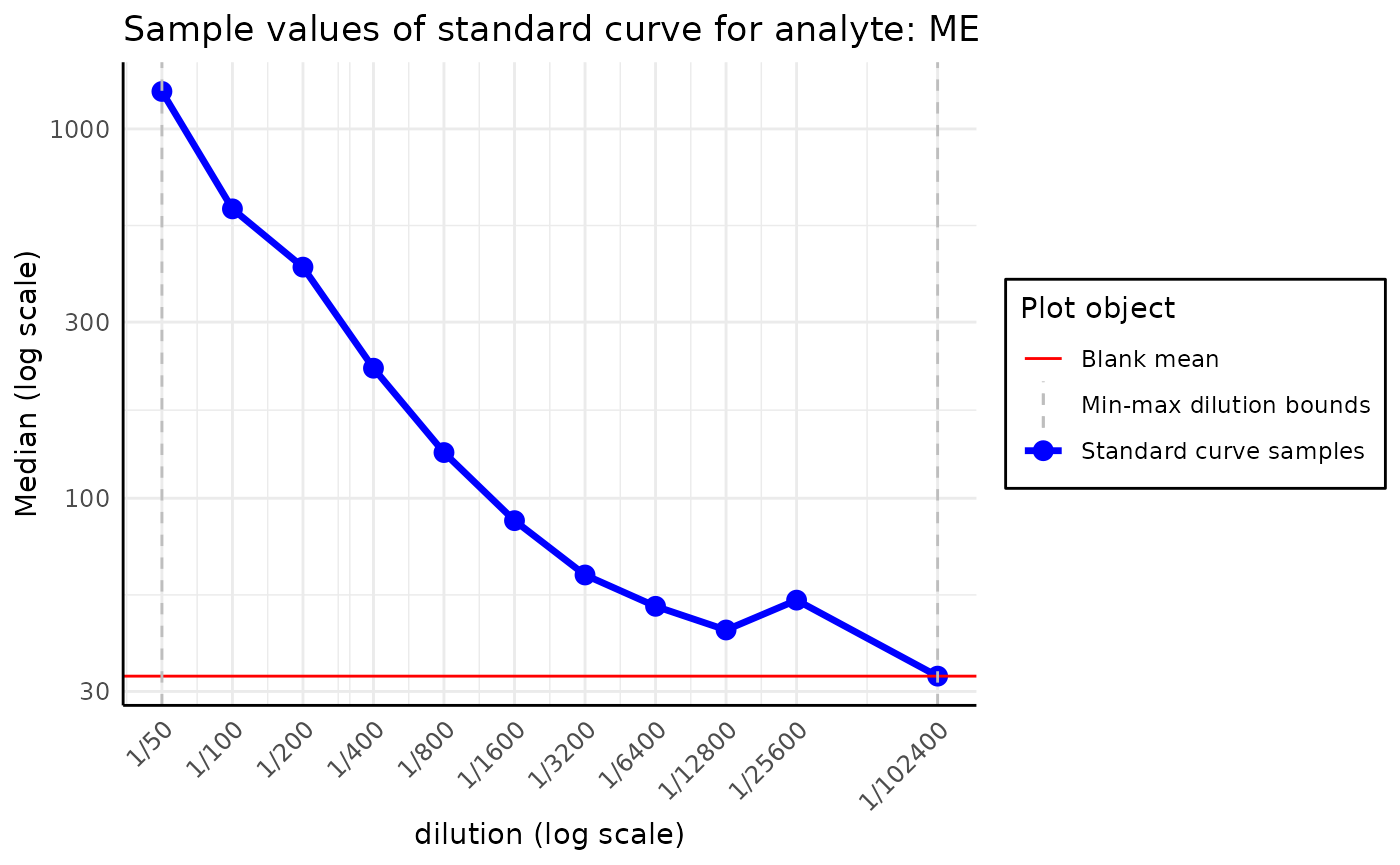

This plot may be used to assess the standard curve’s quality and anticipate some potential issues with the data. For instance, if we plotted the standard curve for the analyte, ME, we could notice that the Median value of the sample with RAU of 39.06 is abnormally large, which may indicate a problem with the data.

plot_standard_curve_analyte(plate, analyte_name = "ME")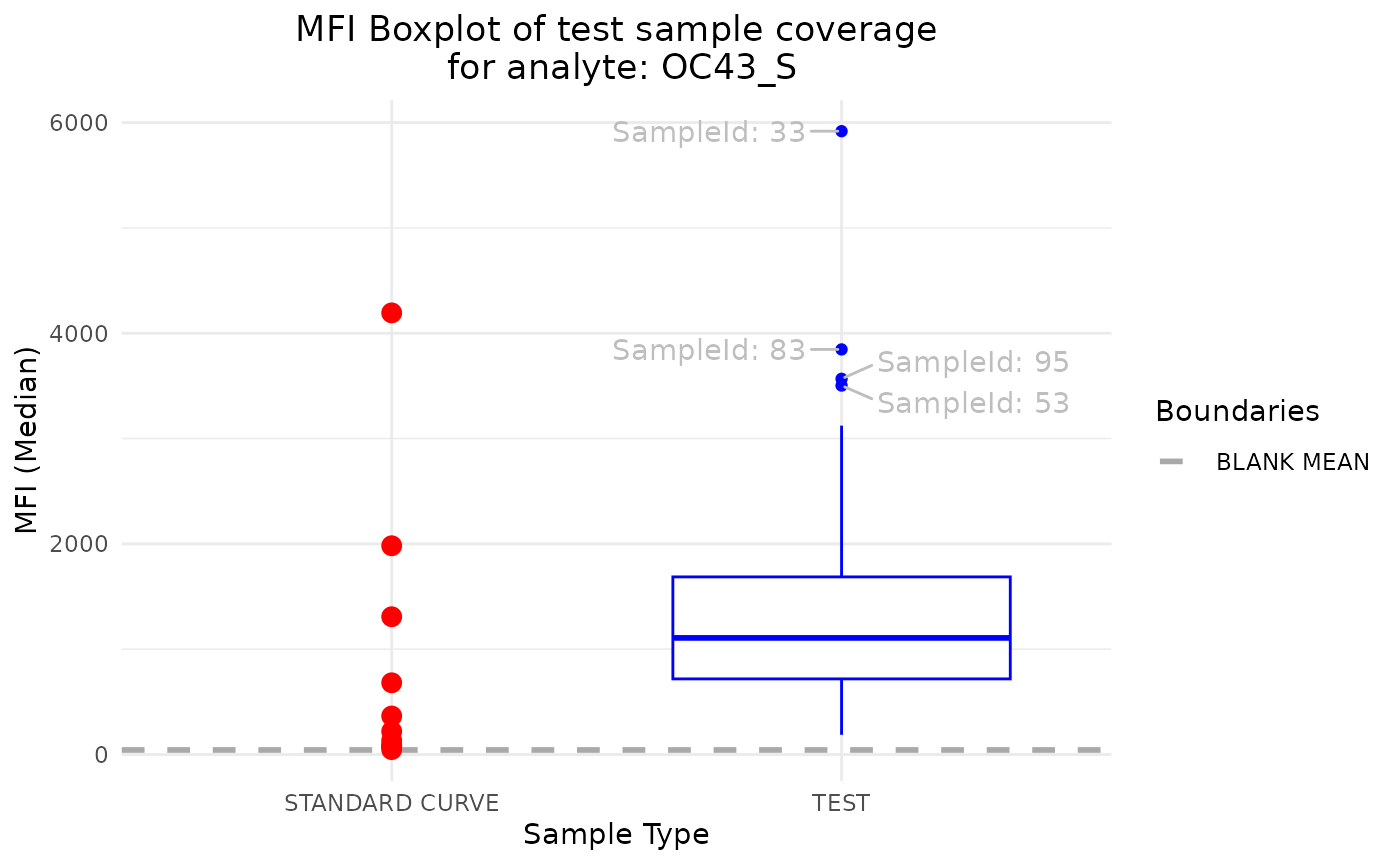

plot_standard_curve_analyte(plate, analyte_name = "ME", log_scale = "all")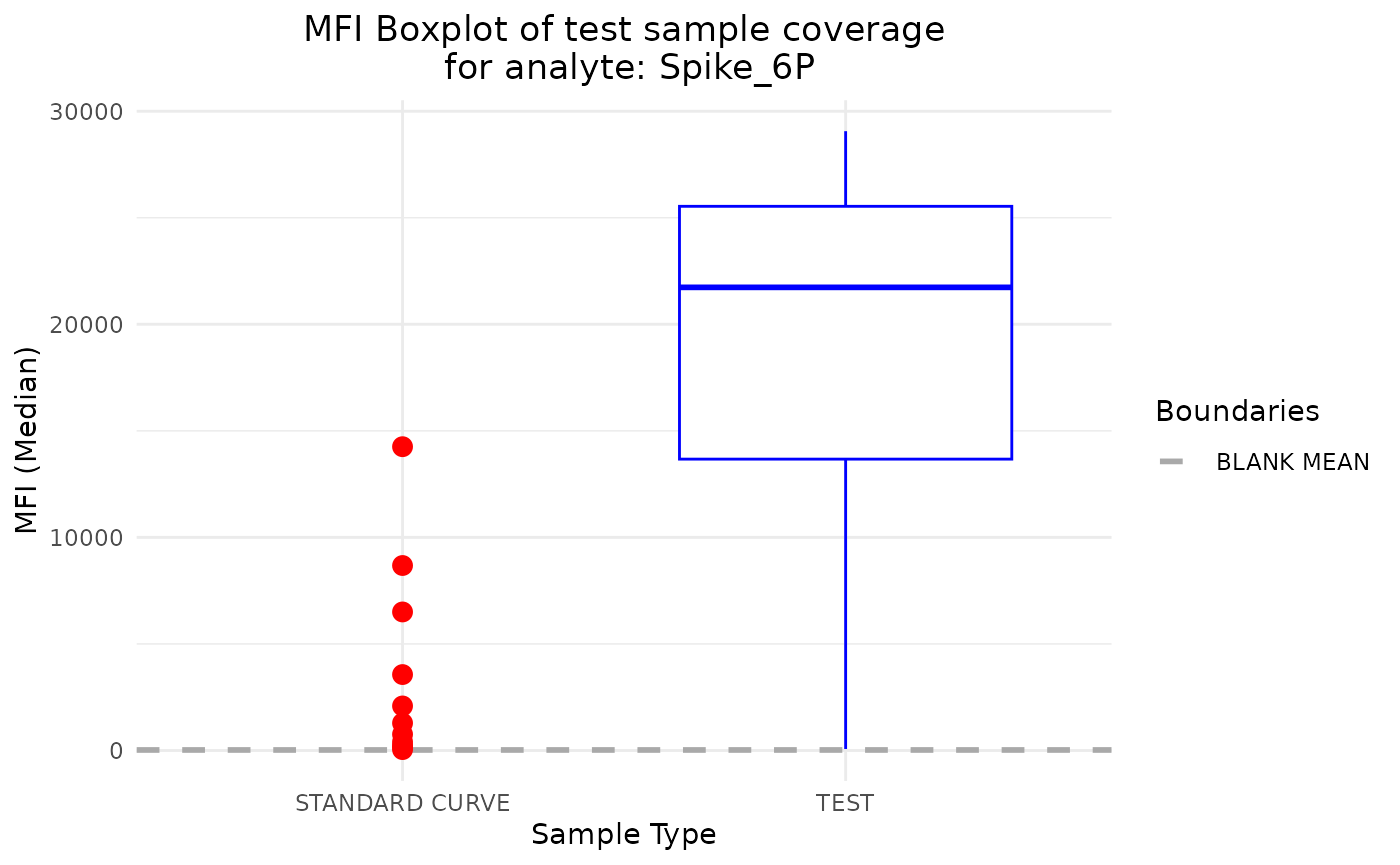

The plotting function has more options, such as selecting which axis the log scale should be applied or reversing the curve. More detailed information can be found in the function documentation, accessed by executing the command ?plot_standard_curve_analyte.

Another valuable method of inspecting the potential errors of the data is plot_mfi_for_analyte. This method plots the MFI values of standard curve samples for a given analyte along the boxplot of the MFI values of the test samples.

It helps identify the outlier samples and check if the test samples are within the range of the standard curve samples.

plot_mfi_for_analyte(plate, analyte_name = "OC43_S")

plot_mfi_for_analyte(plate, analyte_name = "Spike_6P")

For the Spike_6P analyte, the MFI values don’t fall within the range of the standard curve samples, which could be problematic for the model. The test RAU values will be extrapolated (up to a point) from the standard curve, which may lead to incorrect results.

Normalisation

After inspection, we may create the model for the standard curve of a specific antibody. The model is fitted using the nplr package, which provides a simple interface for fitting n-parameter logistic regression models. Still, to create a more straightforward interface for the user, we encapsulated this model into our own class called Model for simplicity. The detailed documentation of the Model class can be found by executing the command ?Model.

The model is then used to predict the RAU values of the samples based on the MFI values.

RAU vs dilution

To distinguish between actual dilution values (the ones known for the standard curve samples) from the dilution predictions (obtained using the fitted standard curve), we introduced into our package a unit called RAU (Relative Antibody Unit) which is equal to the dilution prediction multiplied by a $1,000,000$ to provide a more readable value.

Inner nplr model

nplr package fits the model using the formula:

$y = B + \frac{T - B}{[1 + 10^{b \cdot (x_{mid} - x)}]^s},$ where:

$y$ is the predicted value, MFI in our case,
$x$ is the independent variable, dilution of the standard curve samples in our case,
$B$ is the bottom plateau - the right horizontal asymptote,
$T$ is the top plateau - the left horizontal asymptote,
$b$ is the slope of the curve at the inflection point,
$x_{mid}$ is x-coordinate at the inflection point,
$s$ is the asymmetric coefficient.

This equation is referred to as the Richards’ equation. More information about the model can be found in the nplr package documentation.

Predicting RAU

By reversing that logistic function, we can predict the dilution of the samples based on the MFI values. The RAU value is then the predicted dilution of the sample multiplied by $1,000,000$ .

To limit the extrapolation error from above (values above maximum RAU value for the standard curve samples), we clip all predictions above to $M$ where over_max_extrapolation is user controlled parameter to the predict function. By default over_max_extrapolation is set to $0$ .

Usage

By default, the nplr model transforms the x values using the log10 function. To create a model for a specific analyte, we use the create_standard_curve_model_analyte function, which fits and returns the model for the analyte.

model <- create_standard_curve_model_analyte(plate, analyte_name = "OC43_S")

model

#> Instance of the Model class fitted for analyte ' OC43_S ': 
#>  - fitted with 5 parameters
#>  - using 11 samples
#>  - using log residuals (mfi):  TRUE 
#>  - using log dilution:  TRUE 
#>  - top asymptote: 28414.96 
#>  - bottom asymptote: 38.60885 
#>  - goodness of fit: 0.9970645 
#>  - weighted goodness of fit: 0.9998947

Since our model object contains all the characteristics and parameters of the fitted regression model. The model can be used to predict the RAU values of the samples based on the MFI values. The output above shows the most critical parameters of the fitted model.

The predicted values may be used to plot the standard curve, which can be compared to the sample values.

plot_standard_curve_analyte_with_model(plate, model, log_scale = c("all"))

plot_standard_curve_analyte_with_model(plate, model, log_scale = c("all"), plot_asymptote = FALSE)

Apart from the plotting, the package can predict the values of all the samples on the plate.

mfi_values <- plate$data$Median$OC43_S
head(mfi_values)

#> [1]   43.0 4193.0 1982.0 1308.0  681.0  365.5

predicted_rau <- predict(model, mfi_values)

head(predicted_rau)

#>            RAU    MFI
#> 1     2.375258   43.0
#> 2 20000.000000 4193.0
#> 3  8326.658518 1982.0
#> 4  5240.371360 1308.0
#> 5  2556.577252  681.0
#> 6  1242.668884  365.5

The dataframe contains original MFI values and the predicted RAU values based on the model.

In order to allow extrapolation from above (up to a certain value) we can set over_max_extrapolation to a positive value. To illustrate that we can look at prediction plots. The plot_standard_curve_analyte_with_model takes any additional parameters and passes them to a predict method so we can visually see the effect of the over_max_extrapolation parameter.

model <- create_standard_curve_model_analyte(plate, analyte_name = "Spike_6P")
plot_standard_curve_analyte_with_model(plate, model, log_scale = c("all"))

plot_standard_curve_analyte_with_model(plate, model, log_scale = c("all"), over_max_extrapolation = 100000)

nMFI

In some cases, the RAU values cannot be reliably calculated. This may happen when the MFI values of test samples are way higher than those of the standard curve samples. In that case, to avoid extrapolation but to be still able to compare the samples across the plates, we introduced a new unit called nMFI (Normalized MFI). The nMFI is calculated as the MFI value of the test sample divided by the MFI value of the standard curve sample with the selected dilution value.

nMFI values of the samples can be calculated in two ways - using the get_nmfi function or with the process_plate function that also saves the output into the CSV file by setting the normalisation_type parameter to nMFI in the process_plate function. By default the output will be saved as a file with the same name as the plate name but with the _nMFI suffix.

nmfi_values <- get_nmfi(plate)

# process plate with nMFI normalisation

df <- process_plate(plate, output_dir = example_dir, normalisation_type = "nMFI")

#> Computing nMFI values for each analyte
#> Adding the raw MFI values to the output dataframe
#> Saving the computed nMFI values to a CSV file located in: '/tmp/RtmppxGliI/CovidOISExPONTENT_nMFI.csv'

df[1:5, 1:5]

#>                Spike_6P       ME    HKU1_S   OC43_NP    OC43_S
#> CO-F-226-01-CF 5.842408 1.988889 0.3821903 1.5449180 2.4537445
#> CO-F-263-02-KC 7.171064 1.471111 2.6996681 1.3481967 3.0638767
#> CO-F-080-02-TV 7.169239 2.024444 4.6227876 0.6085246 3.7077827
#> CO-F-215-01-BA 7.586304 3.288889 2.1028761 0.3816393 0.4919236
#> CO-H-SD-039-BC 3.695481 1.037778 1.4778761 0.4393443 0.3340675

Tymoteusz Kwieciński

2024-11-08